As popular as synthetic collateralized debt obligations have become, modeling and pricing these securities continues to provide a number of unique challenges. The value of a CDO tranche depends on both the timing and relationship between any defaults of the individual credits in the underlying portfolio. The market standard for pricing synthetic CDOs is known as the Gaussian time-to-default copula model. In this type of model, the time till a particular name defaults is modeled assuming a Gaussian distribution and the joint conditional probability is calculated using a copula which is a numerical method for constructing a joint probability distribution from marginal probabilities.
Correlations
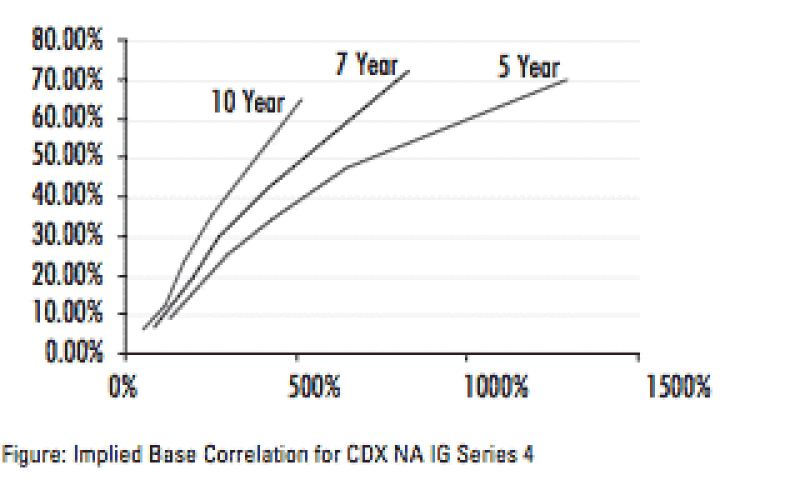
This default correlation is a key model input for synthetic CDOs. Correlations can be derived from historical data or alternatively may be implied from the market. The liquid tranches on credit-default swap indices provide an ideal source for implying correlations in a manner analogous to implying volatilities for options. In this way, a correlation may be implied for a tranche from its market quote. This single correlation--called a tranche correlation--turns out to be difficult to manipulate for several reasons.
Common market best-practice is to imply a different kind of correlation called a base correlation. This is the implied correlation for equity tranches matching the tranche detachment point. A non-equity tranche can be thought of as the equivalent of being long one equity tranche at the detachment point and short a matching equity tranche at the attachment point. A base correlation surface can then be implied from a series of liquidly traded tranches on CDS indices where one dimension is the maturity and the other dimension is the tranche detachment point.
The calibrated base correlation surface is implied from liquid tranches on a defined portfolio of credits. These base correlation surfaces can then be scaled and manipulated to imply prices for non-standard or bespoke CDO tranches for different maturities or different underlying portfolios.
Removing The Basis
In the Gaussian time-to-default copula model, the time to default for each individual name needs to be calculated. Market best-practice is to invert the term structure of survival implied from market quotes on CDS. One issue in this approach, however, is the nature of the differences between the CDS and the CDS indices. A replicating portfolio of CDS typically trade at a basis to the index for several reasons including terms, liquidity and market segmentation.
Market best-practice is to scale the individual survival curves implied from the CDS market so that the replicating portfolio matches the price of the CDS Index.
Implying Base Correlations
Given a base correlation surface calibrated from a set of tranches on one of the CDS indices, we then need to imply base correlations appropriate for the maturity and underlying portfolio of the tranche we want to price.
To imply base correlations for different portfolios we can use one of several techniques. For closely related portfolios, market best-practice is to scale the detachment points so that they are normalized by the expected loss of the original portfolio. To imply base correlations for different maturities, we can interpolate across the base correlation surface. There are several variations in the methods used for interpolation, each designed to better adjust for variations between the distributions of losses for the portfolios underlying each CDO tranche.
Pricing From Base Correlations
Once we have base correlations appropriate for the maturity and underlying portfolio of the tranche, we can then price and calculate sensitivities using the reverse of the logic we used to imply the base correlations from the market.
Putting It All Together
Putting all the steps together, we will review some of the key model assumptions made during this process. A clear understanding of the assumptions behind these types of models is crucial for their correct usage and application.
Step 1. Calculation Of The Marginal Survival Probabilities
This first step consists of implying the term structure of survival for individual credits from market CDS quotes. Common practice is to assume a constant hazard rate model with a fixed recovery.
A number of important assumptions are made during this process. In particular:
* Both the probability of survival and the recovery rate for each credit are assumed to be deterministic. There is no time dynamic and so no capturing of the individual spread volatility.
* It is typically assumed that there is no relationship between the recovery rate and the survival probability. Empirical analysis has shown a strong relationship where recovery rates tend to be lower when survival probabilities are lower (i.e. during a bad economic cycle).
* We cannot easily separate the probability of survival from the recovery rate or any liquidity effect. Typically we specify recovery and liquidity and calibrate the survival probability. This means that any differences in recovery or liquidity will be captured in different implied survival probabilities.
Step 2. Adjusting The Marginals
This next step consists of adjusting the individual or marginal survival probabilities to be consistent with where the CDS indices trade.
Key assumptions include:
* In this step we are pushing all differences between the indices and the CDS quotes into the adjusted survival probability. Some differences may be liquidity for example. All these differences will be reflected in different implied survival probabilities.
* We typically make simplifying assumptions re the term structure of the basis.
* We typically don't take into account any kind of time dynamic for the basis.
* We need to make assumptions re the relationships between sub-indices to keep consistency across related indices.
Step 3. Calibrating The Base Correlation Surface
In this step, base correlations are calibrated from market quotes on liquid tranches on CDS indices.
During this step there are several key assumptions that result from our choice of Gaussian time-to-default model along with our method of calibration of the base correlations.
* Here we are using a model where the correlation is in terms of the time to default. There is no ability to directly incorporate correlation of spreads or hazard rates.
* Different copulas have differing resulting distributions. Choosing a copula which gives a closer fit to the observed distribution of losses for a particular portfolio is more difficult.
* There is no incorporation of individual spread volatility.
* It is more difficult to do sensitivity analysis. The model is calibrated to a particular point of the market. The time dynamic of each of the model inputs needs to be careful considered. For more complex analysis, there is no ability to relate spreads and default which is necessary for any kind of re-investment analysis.
* In the calibration of base correlations, there is no consistent term structure. Each calibration is to a particular maturity and differs across maturity.
Step 4. Pricing Bespoke Tranches
For this final step, attachment and detachment base correlations are interpolated from the base correlation surface and used to price the bespoke tranche.
Again, assumptions re our choice of basket model come into play. There are also a number of assumptions relating to our method of implying and using base correlations.
* Scaling and interpolation of base correlations requires a set of decisions and a clear understanding of the alternate methods is important. For example, two portfolios with the same implied base correlation may have very different underlying credits and characteristics.
* Base correlations have been historically volatile. This relates the time dynamic of the model inputs and calibration. Care should be taken to generate realistic sensitivities.
This week's Learning Curve was written by Rohan Douglas, ceo of Quantifiand adjunct professor of Polytechnic University in New York.





