Range Accruals A range structure accrues value when a reference index fixes inside a specific range during a pre-defined period. It can be used for liability management purposes--as a swap leg versus a money market vanilla interest leg--or for an investment--as a coupon on an exotic EMTN, for example.
The range, determined by two barriers, can remain constant or can have evolving barriers. The expected amount of interest is therefore equal to the maximum coupon times the probability the reference index will stay within the range during the observation period.
A callable (or cancellable) instrument gives the exotic interest rate payer the option to terminate the transaction early on predetermined payment dates. The sale of the option implies an added leverage for the counterparty by enhancing the yield and monetizing the benefit of embedded options.
Technical Characteristics
Unlike the standard interest rate swap, a range accrual swap is a instrument in which the payment of one of the legs depends on the daily fixings of an index being within a specific range. The interest received on each payment date is equal to:
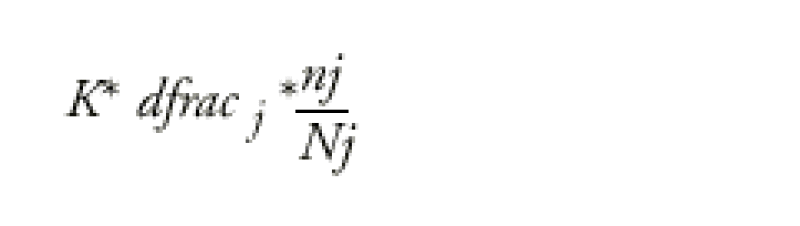
when dfracj is the day count fraction for the Tj - Tj-1 period, nj is the number of days during the observation period when the index fixes within the range (in relation to Tj & Tj-1) and Nj is the total number of days in the observation period.
Note K could be a fixed rate, a money market rate or a swap rate.
Thus, if K is fixed, the net present value of the exotic leg has the form:
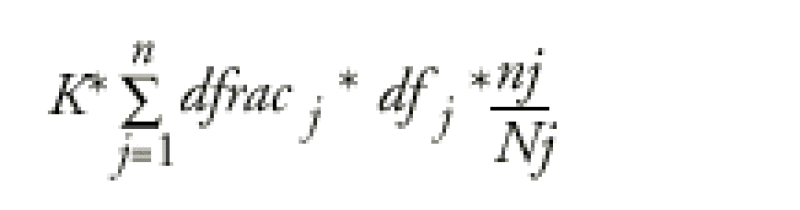
when dfj is the discount factor at time Tj.
Cap & Swaption Volatility
In a callable range accrual structure, two volatilities must be considered.
If the investor's coupon depends on the daily fixing of a money market rate, we first have to consider the volatility of a cap with, for example, three-month LIBOR as the underlying.
The higher the volatility of this index, the lower the probability the index will stay between the two barriers (for periods when the forward rates lie within the barriers). The lower the probability of being inside the range, the higher we can set the level of K (the maximum coupon). The investor is short the cap volatility.
Nevertheless, it is possible the forward money market rates are outside the range (often the case for the last few periods of the structure). For these periods, the higher the volatility of the index, the higher the probability the index will move inside the barriers and K will be paid. In this case the investor will be long the cap volatility for this period.
The second volatility to take into account is the swaption volatility.
An option that can be exercised on any one of several dates is a Bermudan option. In order to estimate the value of this option according to the market conditions, the implied volatility of the option must be adjusted on the volatility smile of a string of swaptions expiring at each call date with the remaining years to maturity as an underlying swap.
The investor, short the option to cancel the transaction early, is therefore short the swaption volatility.
As a result, when an investor buys a callable range accrual, he implicitly sells short-term and long-term volatility when the forwards lie within the defined ranges.
Estimation Of The Range Accrual Probability
We recall the form of the exotic leg:
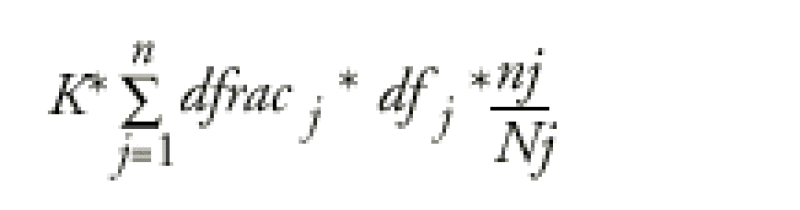
should be understood to be a probability.
It can actually be written when
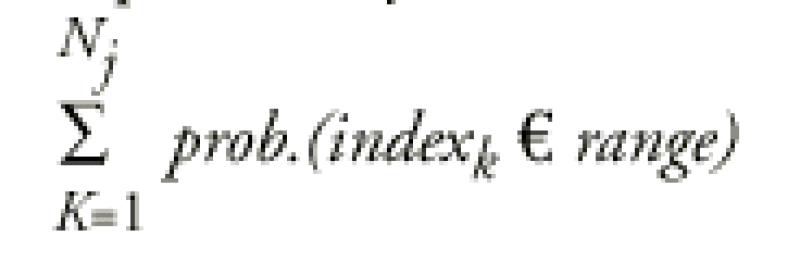
Nj is the numbers of days of the jth observation period.
In order to get an idea of how to estimate this probability we consider the example below:
An exotic interest leg pays an annual interest rate proportionate to the number of days the three-month dollar LIBOR lies between K1 and K2 (K1<K2).
Ri is the value of the three-month LIBOR on day i, the probability P of the index being between the barriers K1 and K2 at time ti is:
P = prob(Ri>K1)-prob(Ri> K2)
In this way, the exotic leg can be represented as a string of binary options, one for each day of the life of the product. Each day Ri fixes outside the range, the exotic leg receiver loses one day of interest (notional*K /Nj), with Nj the number of days of the jth observation period.
Yet, we need to take into account the fact that, as the index used for the binary option at ti is paid at the first payment date after ti, we need to time adjust the value of the forward and as a result the probability. Consequently, P becomes P* = P x convexity adjustment.
Thus, the present value of a binary option that matures at ti is equal to:
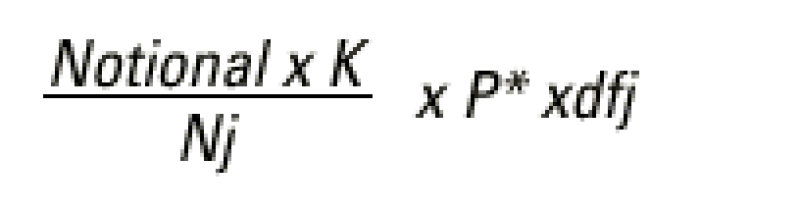
In order to have an overview of forward distribution in the euro and the dollar market, we show next the normal volatility distribution of the three-month Euribor and of the three-month dollar LIBOR forwards on three different dates.
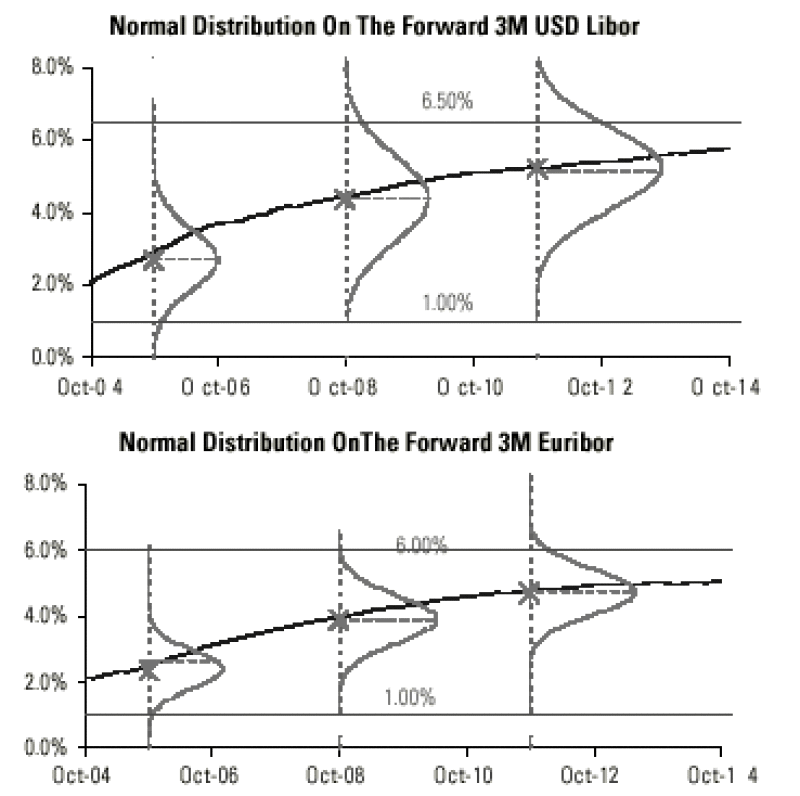
The shape of the tail of distribution simply reflects the higher volatility of the dollar market and consequently the higher probability for the three-month dollar LIBOR to fix outside the range.
Sensitivity Analysis
A range accrual swap pays a higher coupon and is, therefore, more popular when the curve is steep (or steeply inverted) and/or cap volatility is at a high level. Indeed, these conditions increase the probability of the index fixing outside the range leading to a higher coupon for the investor. In the same way, the narrower the range the larger the coupon.
Market Opportunity & Investor Forecast
Recently, the U.S. market has found itself in the specific market conditions mentioned above. Investors therefore showed interest in this type of structure, mainly with a lower barrier at 0% and a higher barrier either fixed or stepping up over time, following the shape of the forward curve.
Clearly, in this case, the investor will be rewarded as long as the realized rates consistently fix below or around the forward rates seen from today.
By entering into such a structure, the main belief the investor has is the Federal Reserve will tighten to some extent, but less than predicted by forwards, and the curve will flatten.
If this proves to be the case and rates remain lower than the forward curve predicts, the option to call or to cancel the trade by the issuer is likely to be exercised. Therefore, by adding the callable feature, the investor leverages the view he has when entering into a regular range accrual, but benefits from the added premium coming from the sale of the option.
If the short end of the curve stays the same or the curve flattens and the option is exercised, the investor will have benefited from receiving a high coupon--sometimes more than four times the market rate.
Example
The following example takes a callable range accrual indexed on three-month USD LIBOR, with step-up barriers as follows:
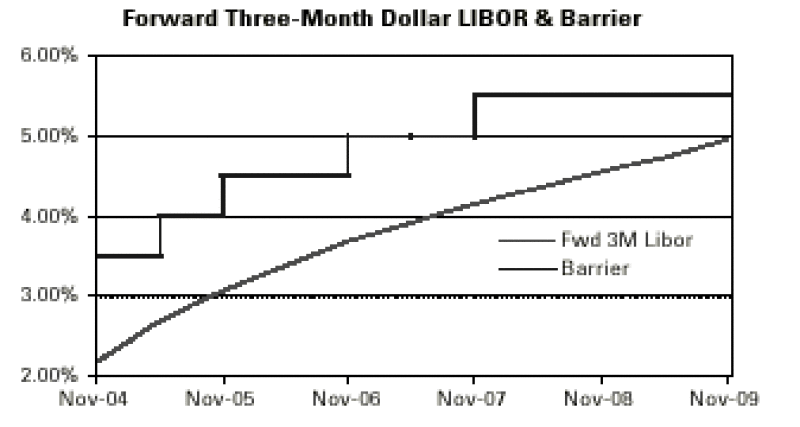
The coupon paid is [USD LIBOR + margin] x (n/N) and the maturity is five years.
Different Market Scenarios
As we saw earlier, the probability the index will fix in a specific range depends on:
* the level of interest rates and the shape of the yield curve
* the level of volatility and the shape of the volatility curve
* the width of the range
* the maturity
* the issuer's credit rating
To illustrate how the price is linked to each parameter, we propose to observe the change in the price of the note if shifts in the yield curve and volatility happen immediately. The yield curve scenarios are as follows:
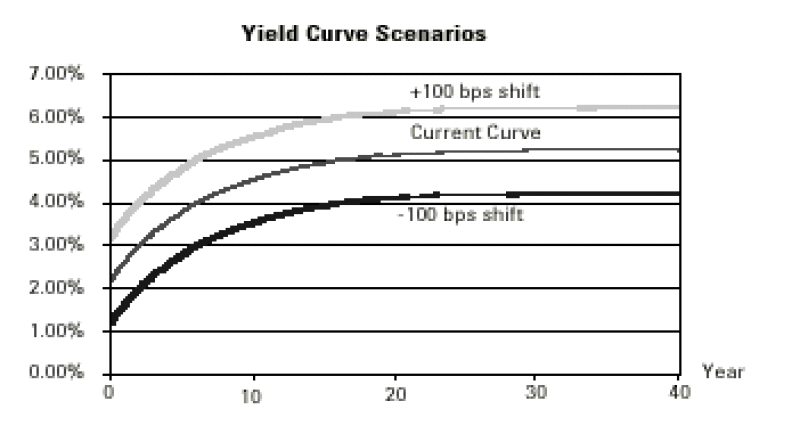
* the yield curve is shifted up by 1%
* the yield curve is shifted down by 1%
The volatility scenarios are as follows:
* swaption and cap lognormal volatility up by 10%
* swaption and cap lognormal volatility down by 10%
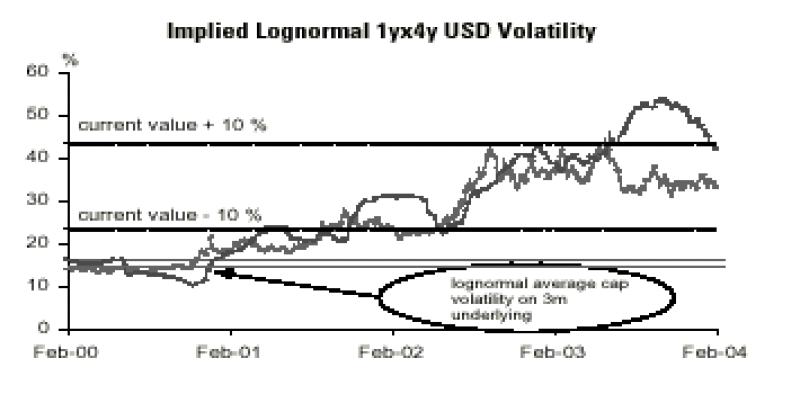
The following graph shows the implied lognormal volatility of a 1yX4y USD swaption and the lognormal average cap volatility on six-month dollar LIBOR.
The table below shows the effect of each scenario and the combination of rates and volatility shift on the price of the structure.
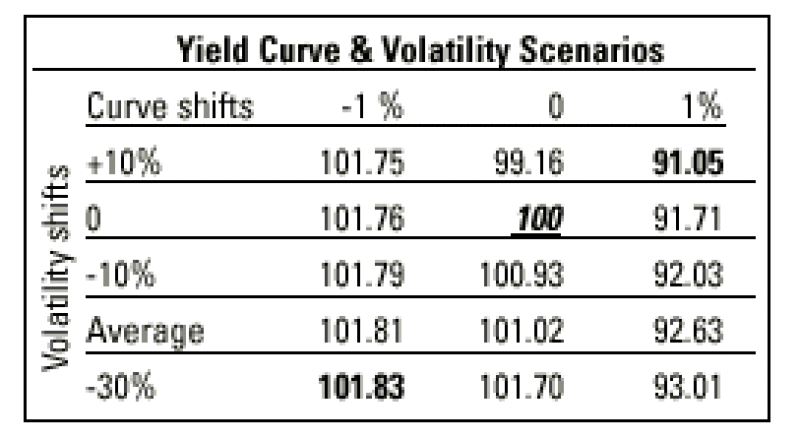
The best scenario occurs when the rates go down and the volatility goes down. This is because the forward rates are further inside the range and the lower volatility makes it less likely they will move outside the barrier.
But in the best scenario, the price of 101.83% indicates the high chance the issuer will call the note on the first call date (in this case in one year).
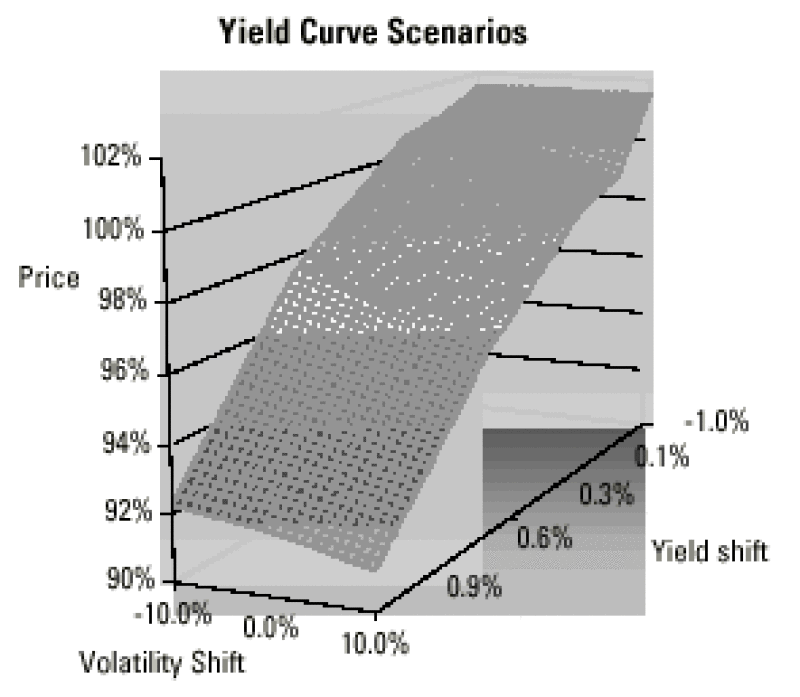
The worst situation occurs when the yield curve reaches its higher level and the volatility is higher. In this case, the forward rates are well outside the range, so the expected coupon is small and because the volatility is higher there is a chance the rates will go even higher.
Moreover, we must remember that besides parallel moves, other market parameters can influence the price of the note, such as the credit worthiness of the issuer or the shape of the volatility smile. In addition, a steepening of the yield curve will decrease the price and a flattening will increase the price.
This week's Learning Curve was written by Nicolas Caseris, a structurer in the interest rate derivatives group at BNP Paribas in London






