The rapid growth of credit correlation products such as single-tranche CDOs has in part been the result of improvements in analytics allowing the risk of such products to be managed with greater accuracy and efficiency. In this article we describe the behavior of tranche Deltas--a measure of spread risk--as both structural and market features of the CDO move.
An ideal hedge for a dealer who has bought protection on a single-tranche CDO would be an identical offsetting transaction. However, the bespoke nature of the market makes such transactions unlikely. As a result, a dealer will focus on managing the spread risk of a single-tranche position via the underlying default-swap market.
Defining Delta
All single-tranche positions are subject to mark-to-market movements as credit spreads on names in the underlying portfolio shift. To hedge the spread risk of a short (long) position in a tranche, a dealer needs to sell (buy) protection on each of the underlying credits in the portfolio according to the Delta (d) measure.
We define the Delta of a credit in the CDO as the amount of protection the dealer sells (buys) on that name to hedge the market-to-market risk of a short (long) tranche position due to changes in the spread of that name.
Delta of Credit = Change in Mark-To-Market of Tranche
Change in Mark-To-Market of Credit
This relationship defines the percentage of the notional of the credit used for hedging.
Deltas are calculated using brute force by shifting the spreads on each individual name in the CDO by a small amount (1-10bps), and then calculating the market-to-market change of the tranche. Deltas range from 0%-100% for a credit in a CDO. The Delta of a 0%-100% tranche of a CDO is 100%.
A delta-hedged tranche is not a perfect static hedge however, and the tranche is still subject to risks such as Spread Convexity for larger spread moves. Due to this, the Deltas need to be rebalanced throughout the life of the transaction (Dynamic Hedging). Because of the cost associated with frequent rebalancing, dealers are motivated to do trades that reduce these additional risks such as placing other tranches of existing CDOs or entering into similar offsetting transactions.
Delta Sensitivities
Deltas of individual credits depend on the following parameters and will change as these parameters change through the life of the transaction:
*Subordination and Width of the Tranche
*Spread of CDO Credits and Relative Spread Movements
*Time Remaining until Maturity
*Correlation Assumption
*Recovery Rate Assumption
In order to understand the directionality and magnitude of Deltas we introduce two CDO examples. The collateral pool consists of 50 CDS with each credit having a EUR10m notional, 100bps spread and recovery of 35%. We define a Discrete CDO with equity, mezzanine and senior tranches of 4% width and a Super Senior tranche of 88%. We also define a Continuous CDO on the same collateral pool in which each tranche has a 1% width and attachment points vary by 1% increments.
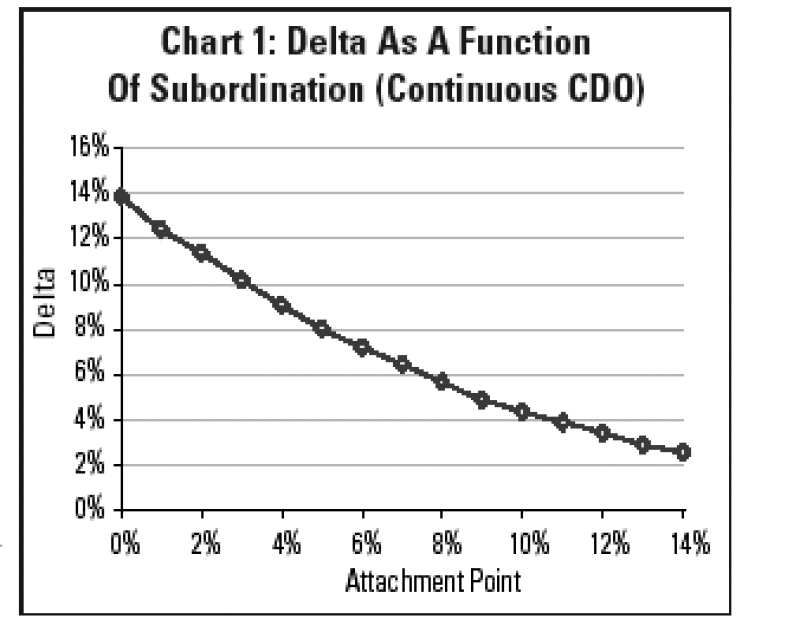
Delta as a Function Of Subordination
Tranches lower in the capital structure are riskier as there is less subordination to act as a buffer against defaults. As the equity tranche is the riskiest tranche, credits in the underlying portfolio have the highest equity-tranche Delta relative to the more senior tranches. For more senior tranches, the Delta of a credit is lower. As Delta can be thought of as representing the probability of losses in a tranche, tranches with less subordination have a higher Delta.
Delta as a Function of Credit Spreads
One way to conceptualize Delta is to think of ordering the credits in the CDO by their time to default. For constant recovery and correlation, this will be a reflection of the spread of the credits: credits with a higher spread are expected to default before credits with a lower spread. If a credit whose Delta we are calculating is toward the front of this 'queue' (i.e. higher spread) it is more likely to cause losses to the equity tranche and so its equity tranche Delta will be higher. If the credit is further back in this queue (i.e. lower spread) then its equity tranche Delta will be lower. As credits further down the queue are expected to default later, they are more likely to cause losses to the senior tranche and the senior tranche Delta of the credit will rise.
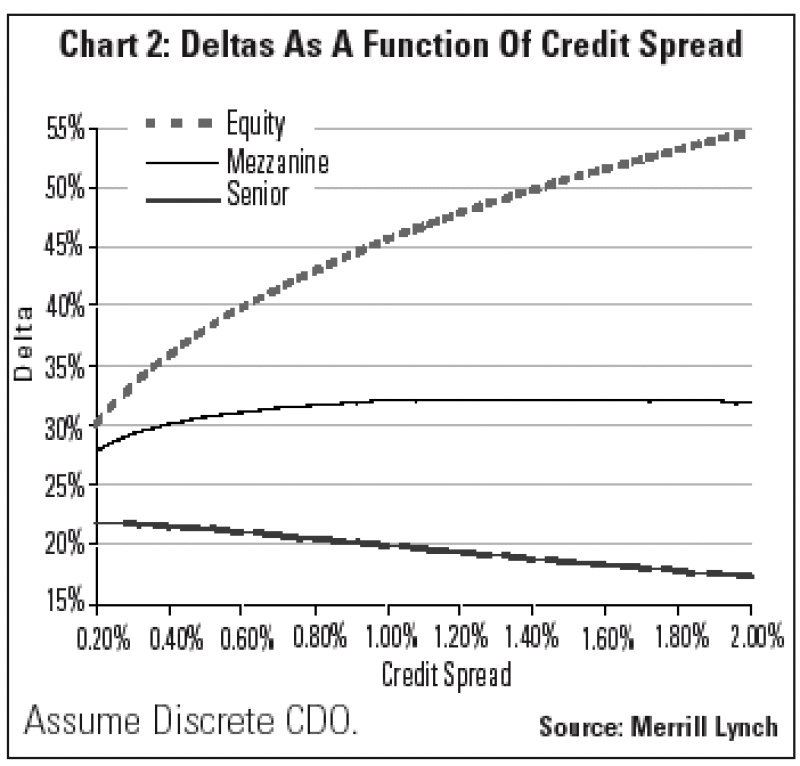
These results also apply to the directionality of Delta when credit spreads in the portfolio move over time.
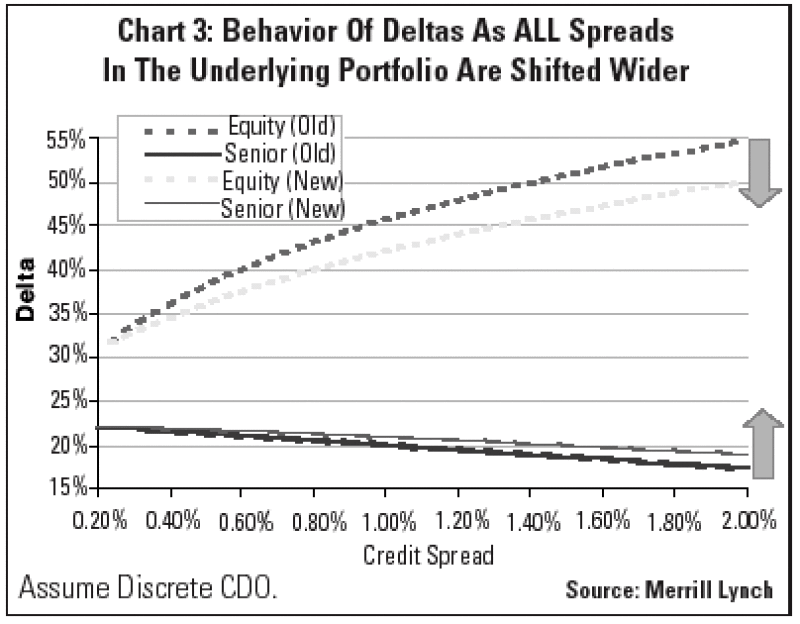
Delta As A Function Of Cumulative Spread Moves
The cumulative spread movements of all the credits in the CDO will also impact how the Deltas change. We analyze how Deltas move by shifting all credit spreads in the above example wider by 25bps. As can be seen in Chart 3 this has the impact of decreasing the equity tranche Deltas for each individual credit, but increasing the senior tranche Deltas for eachindividual credit. Similarly, when all credit spreads in the CDO are shifted tighter then the equity tranche Deltas increases for each individual credit and the senior tranche Deltas decreases for each individual credit. The shape of the distribution of Deltas remains the same after cumulative spread movements though.
Delta As A Function Of Time
Deltas will also change due to the passage of time even if spreads remain unchanged. Assuming no defaults in the underlying portfolio, the Delta of the equity tranche will increase to 100% as maturity approaches and the Deltas of the mezzanine and senior tranches will decrease to 0%. As maturity approaches, the more senior tranches become relatively less risky compared to the equity tranche, as there is less time for defaults to accumulate such that the mezzanine and senior tranches are reduced.
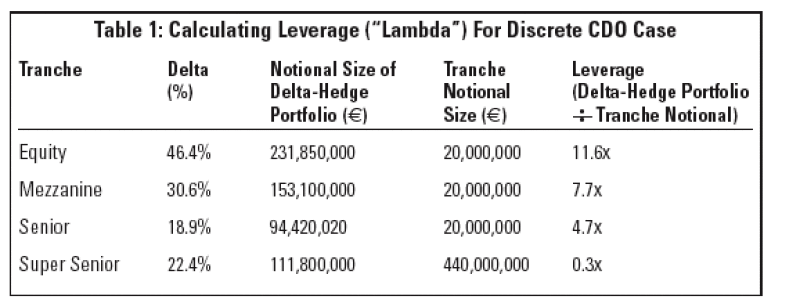
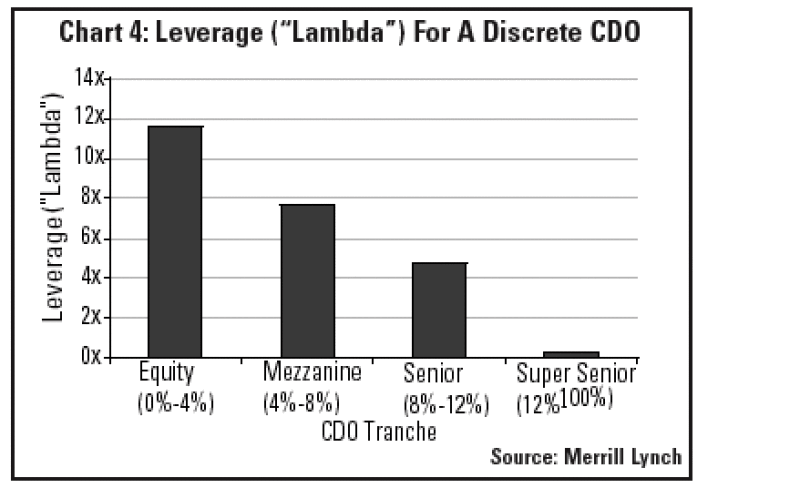
Leverage Of A Tranche
The Leverage of a tranche is an important spread risk measure. We define Leverage as the notional size of a tranche's Delta-hedge portfolio divided by the tranche's notional size. Table 1 shows the calculation of Leverage for the Discrete CDO example. Effectively, Leverage scales the Delta by the notional size of the tranche: the Delta of the super-senior tranche is actually larger than the Delta of the senior tranche, but its Leverage is smaller. More leveraged tranches are those for which the spread risk is high in relation to the notional.
Delta-Hedging A Standardized Tranche
With A CDS Index
While underlying CDS will typically be used to delta-hedge a bespoke single-tranche position, standardized tranches of CDS indices can be delta-hedged via the underlying index itself. Suppose that a dealer buys protection on the 7%-10% tranche of iBoxx CDX NA with a USD30 million notional. Suppose also that the tranche has a Leverage of 5x, then an iBoxx CDX contract size of USD25 million would imply a delta-hedge of 6 contracts. Note that this hedge is an average delta-hedge. As iBoxx spreads are dispersed, for a senior tranche the tighter names (with higher than average Deltas) would be underhedged whereas the wider names (with lower than average Deltas) would be overhedged. The reverse would be true for hedging an equity tranche position with the index.
 |
| Barnaby Martin |
 |
| Atish Kakodkar |
This week's Learning Curve was written by Barnaby Martin
and Atish Kakodkar in credit derivatives research at
Merrill Lynch .





