In this Learning Curve we value the so-called loss cap, an important structural feature that distinguishes synthetic collateralized debt obligation squareds from synthetic CDOs. The CDO2 market has grown rapidly because market participants are using higher leverage to achieve spread targets in the face of credit spread tightening. We estimate USD100 billion in tranche (notional) of public CDO2s was issued last year, a 25% increase from the year before.
What Is A CDO2?
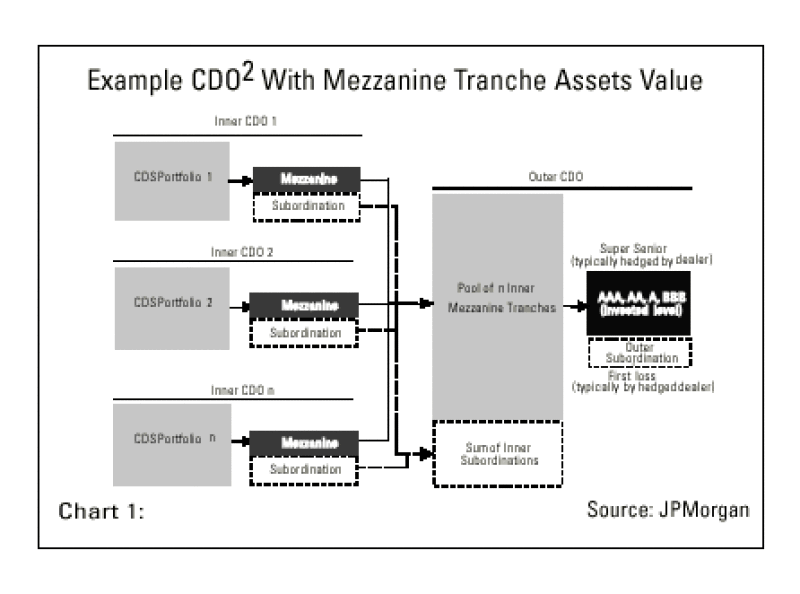
Chart 1 illustrates a CDO2. In our illustration, there are several inner CDOs, with a bespoke inner tranche carved out of each inner CDO. Together the inner tranches form the assets. On the liability side is the outer CDO, equal in size to the portfolio of inner tranches. Outer tranches of different risk--whether measured by rating or spread--are created from the outer CDO for end investors.
A typical inner tranche references a portfolio of 80-120 equally-weighted corporate credit-default swaps. CDO2s comprise anywhere from three to 20 inner tranches with eight-10 being the most common. Our illustration shows mezzanine inner tranches, which are more prevalent in contemporary structures because they offer spread pickup versus senior tranches and are less leveraged than equity tranches.
The outer CDO is equal to the sum of the notionals of the inner tranches. Outer tranches customized for end users are carved from the outer CDO. The outer CDO has additional subordination equal to the sum of the subordinations of the inner tranches. The reason we talk about the sum of the subordinations of the inner tranches is because our example benefits from cross subordination, a feature that has started to appear in CDO2s. Cross subordination means losses in a deteriorating inner tranche can be offset with remaining subordination from other inner tranches. Inner tranches share subordination. As long as there is subordination available for any inner tranche, losses are not passed to the outer CDO. Assuming cross subordination, there is only loss on the outer CDO if:
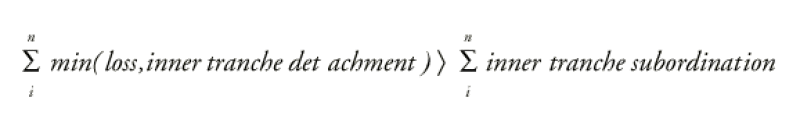
We assume cross subordination to compare a CDO2 to a thin tranche on a large portfolio and, in the process, value the loss cap that differentiates CDO2s from less complex CDOs.
How Is A CDO2 Different From A Highly Leveraged CDO?
A question investors typically ask is, "How is a CDO2 different from a thin tranche of a large portfolio or a large CDO?"
While at first glance these two structures seem the same, they are not. We have already discussed how losses in a CDO2 are capped by the detachment points of the inner tranches, but for typical structures, such as mezzanine inner tranches, the loss cap tends to be more beneficial for senior exposures. If we assume cross subordination, it's possible to compare a CDO2 to a large CDO because we can scale subordinations of the inner tranches on a linear basis and add them up, to ensure that both structures have the same aggregate subordination. In our case study we assume the following parameters for a CDO2 with cross subordination:
* 10 inner portfolios, each is EUR1 billion in notional;
* Average rating of inner portfolios is A2 to A3;
* Average underlying CDS spread of inner portfolios is 45-55 basis points;
* Average overlap among inner portfolios is 27.5%; and
* 5 year maturity.
To construct an equivalent large CDO we group the inner CDO portfolios into a large portfolio. To determine an equivalent tranche, we scale size and subordination depending on the outer tranche of the CDO2. How could we create a large CDO tranche assuming a 50-60% outer tranche and 3-6% inner tranches for the CDO2?
We first determine the attachment point for the large CDO tranche. Since the inner 3-6% tranches share subordination, we treat them as a combined unit and aggregate their subordinations, 10 * EUR30 million = EUR300 million. We also need the size of the outer CDO, 10 * EUR30 million = EUR300 million, to determine the second level of subordination provided by the outer tranche. The second level of subordination for the outer 50-60% tranche, 50% * EUR300 million = EUR150 million, combined with the aggregate subordination of the inner tranches, is EUR450 million. Since the aggregate size of the 10 inner CDO portfolios is EUR10 billion, the attachment point of the large CDO tranche is 4.5% based on this notional.
The process is repeated using the detachment point of the outer tranche (60%) to determine the detachment point of the large CDO tranche (4.8%).
Both the CDO2 outer tranche and the large CDO tranche have the same underlying credit exposure of EUR10 billion. Both also have a size of EUR30 million and a subordination of EUR450 million, so we can compare them.
Default Sensitivity
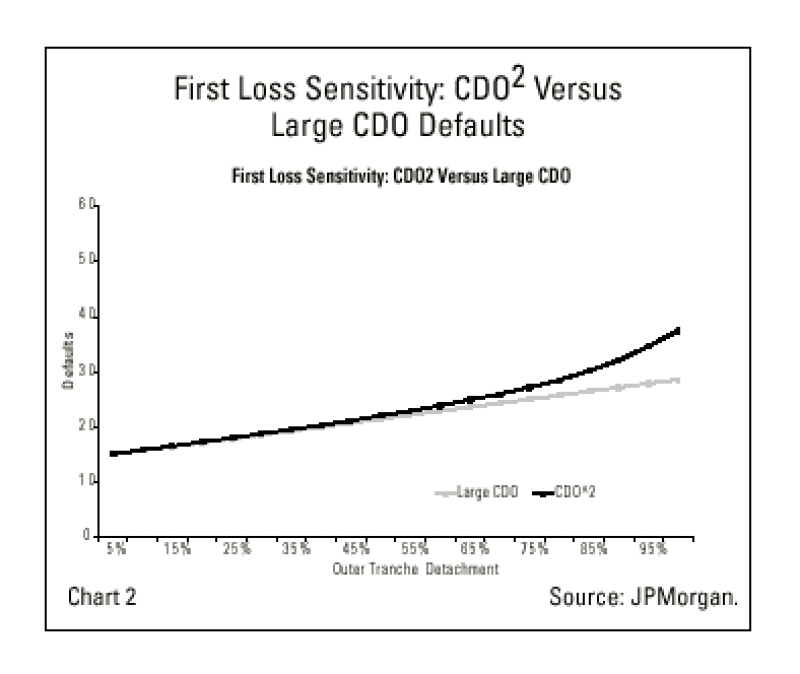
We assume a series of 5% thick outer tranches for the outer CDO, for example 0-5%, 5-10%, and so on, versus scaled tranches for the large CDO; with 3-6% inner tranches, equivalent large CDO tranches are 3-3.15%, 3.15-3.30%, etc. Using a model, we randomly default names at 40% recovery. Chart 2 plots the probability-weighted number of defaults needed to register a first-loss for the comparable tranches assuming 3-6% inner tranches. To show both series on the same x axis, we convert large CDO tranches back to equivalent CDO2 outer tranches.
Since inner CDO losses are capped by the 6% detachment points of the inner tranches, losses are not linear as in the case of the large CDO and this dynamic is observable at the senior end. In CDO2s, the existence of inner tranche detachment points causes loss capping, while the distance between inner tranche attachment and detachment points accentuates loss capping. If instead of 3-6% inner tranches we assume 3-7% inner tranches, the higher detachment points would likely delay the effect of the cap, all things being equal. There are many variations on this theme and investors can use the example provided as a basis to evaluate transactions.
Ratings Sensitivity
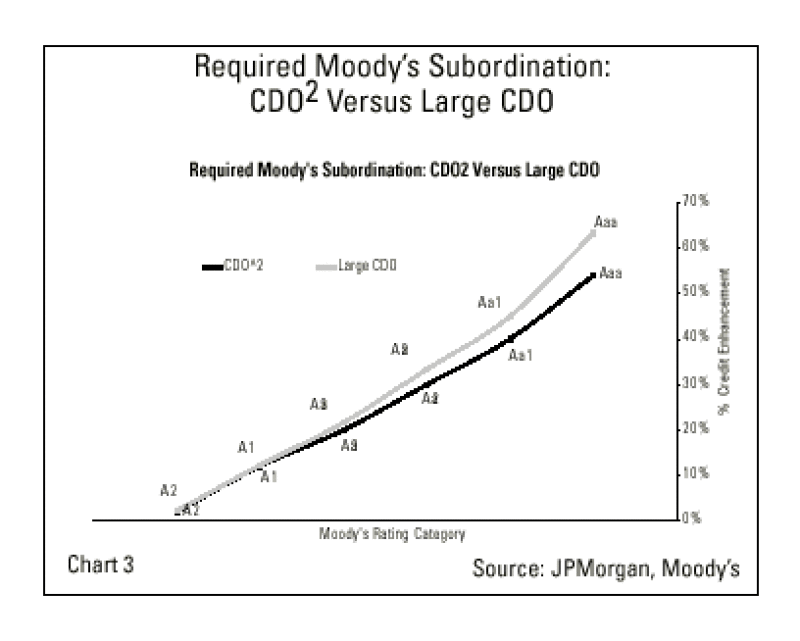
From a ratings perspective, Chart 3 compares the minimum subordinations from Moody's Investors Service's model output between the CDO2 and the large CDO. The rating agencies recognize the capped loss benefit by requiring lower attachment points for the same rating in the case of the CDO2, most visible at the Aa1 to Aaa level in our example.
Pricing Sensitivity
Chart 4 compares model-based pricing. This particular analysis is dealer model-dependent and does not factor in costs. The model spread for the CDO2 diverges from that of the large CDO toward the senior end.
Putting It All Together
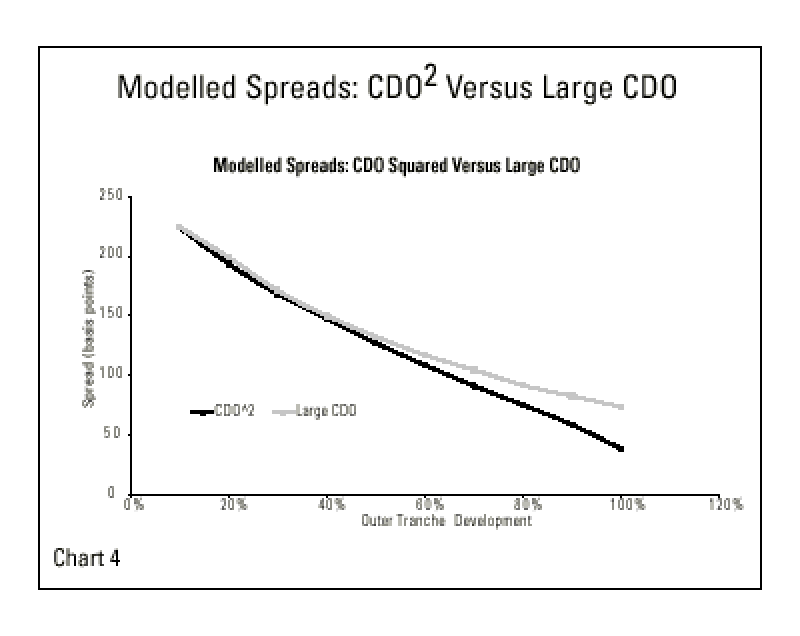
Due to the customized nature of synthetic CDOs and in particular CDO2s, it's difficult to form broad conclusions. But we can reasonably say that in CDO2s with cross subordination, compared to less complex large CDOs, senior tranche investors would benefit the most, while mezzanine tranche investors benefit the least from the loss cap, which is also suggested by our ratings and pricing examples.
This week's Learning Curve was written by Christopher Flanagan, managing director and head of global structured finance research at JPMorgan, and Rishad Ahluwalia, Benjamin Graves, and Edward Reardonin global structured finance research at JPMorgan.
| |
| Christopher Flanagan |
| |
| Rishad Ahluwalia |
 |
| Benjamin Graves |
 |
| Edward Reardon |






