In this paper, we propose a new methodology for quoting loss baskets and potentially diversified first-to-default baskets in a consistent manner that overcomes the problems associated with Gaussian copula models. We find that the model calibrates reasonably well to the five year and 10 year iTraxx Europe tranches, the five year and 10 year iTraxx North America tranches and the standardised, diversified first-to-default baskets quoted in the broker market. In light of these results, we postulate that the model should also be extendable to bespoke portfolios. In this first part we introduce the Composite Basket Model and describe its implementation. In next week's issue we will present some results and show how the model can be used to price bespoke baskets with skew. Gaussian Copula & Correlation Skew
The Gaussian copula approach has proven popular in the pricing of basket tranche products. This success can mostly be attributed to the simplicity and efficiency of its implementation (a comparison may be drawn with the Black Scholes model used in option pricing). The key inputs to the model, however, are default correlations, which are not directly observable. These parameters can be inferred from historical equity prices, asset swaps spreads or default swaps levels, but none of these is particularly satisfactory.
Alternatively, a single (average) correlation for each tranche can be implied from market prices. Unfortunately, when correlations are implied from all of the tranche prices observed in the market, each tranche typically has its own individual correlation, which is different from the others. Specifically, we find that the market charges relatively more for equity or senior tranches and much less for mezzanine tranches than this model implies. This is often explained in two ways. On one hand there is a supply and demand argument that investors are nervous of the risk inherent in equity tranches while mezzanine tranches are extremely popular with investors and sellers of protection on senior tranches seem to require a minimum coupon irrespective of subordination. On the other hand the Gaussian copula loss distribution underestimates the perceived chances of an extremely low or high number of defaults whilst significantly over-estimating the chances of observing a few defaults.
In practice the independent calibration of the Gaussian copula model to each individual tranche gives rise to a correlation "skew", "smile" or "smirk." Its existence presents two serious problems. The first problem is a conceptual one: the correlation parameters of the copula are asset specific quantities and not tranche specific ones and therefore ought to be the same irrespective of the tranche being priced. The second problem is more practical: the sensitivity of a tranche to the correlation parameters is strongly related to its position in the capital structure. While equity tranche spreads drop with an increase in correlation, senior tranches behave in an inverse manner. In turn mezzanine tranches are not very sensitive to correlation at all. Figure 1 illustrates this aspect.
Figure 1: Implied Gaussian copula correlation Vs. breakeven coupon for four of the iTraxx Europe tranches.
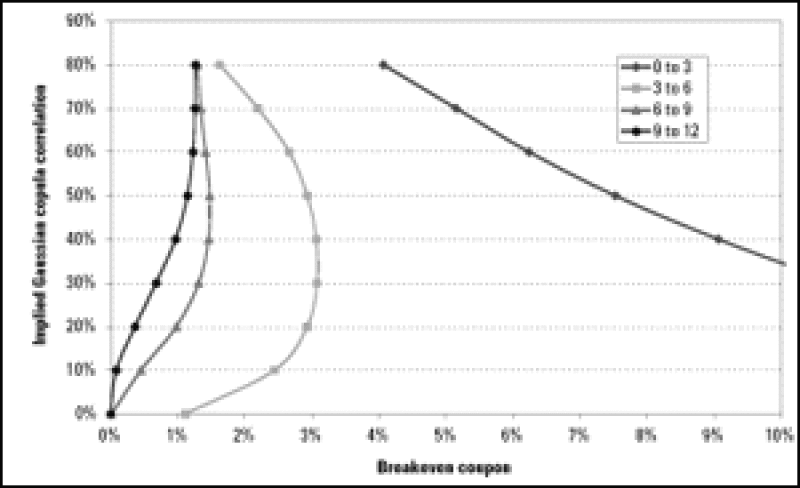
This fact creates a serious problem for the pricing of tranches because even small changes in the spread of a mezzanine tranche can cause large swings in the corresponding correlation. In addition, the correlation may not be unique (two different correlations may produce the same price) and in extreme cases it may not even be possible to find a correlation value that corresponds to the observed price.
Several approaches have been proposed to overcome this problem. For example, several authors have looked at the effect of assuming that some of the input parameters are random (see for example [1]). Others have tried alternative copulas [2] or stochastic intensity models (for example [3] and [4]). None of these approaches, however, has become widely accepted and the problem remains. Most notably an alternative calibration scheme was recently proposed where the calibration is applied to multiple first loss tranches covering the relevant part of the capital structure [5]. This approach relies on interpolation between published quotes and it is not clear how it can be generalised to the pricing of bespoke tranches.
Composite Basket Model
We propose an approach that relies on the commonly held intuition that investors allocate the risk in a given credit to different "buckets": some of the risk is driven by the particular sector, which can be a country and/or an industry group; some is specific to the company in question; and some is driven by some form of market consensus on the general outlook of the economy. We then model the first two with independent Poisson processes (respectively the systemic and idiosyncratic processes) and the latter through the Gaussian copula (we will refer to this as the copula term). We named the method the Composite Basket Model, or CBM.
More formally, given the probability of survival of an asset, p(t), and one systemic sector only, we write:
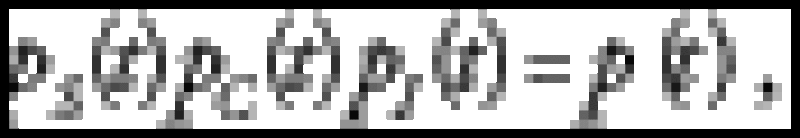
where pS(t),pI(t) and pC(t) are respectively the systemic, idiosyncratic and copula survival probabilities. At least in the case of a flat intensity curves we can interpret this as a linear combination of spreads:
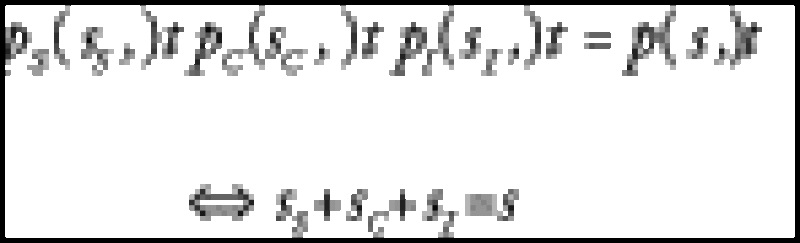
In the simple case of N assets with identical probabilities and unity loss amounts, the loss distribution, conditioned on the systemic and copula terms, Xs and Xc respectively, is:
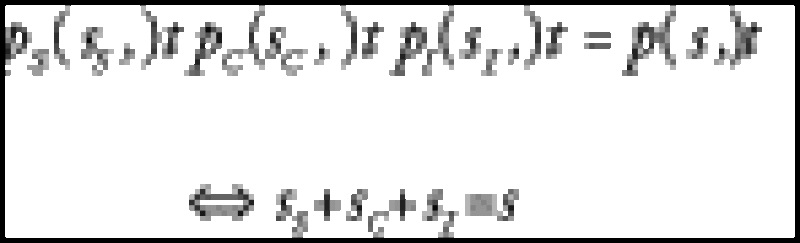
where we dropped the time argument for simplicity of notation. The default probabilities then expand, as postulated by our model, into:
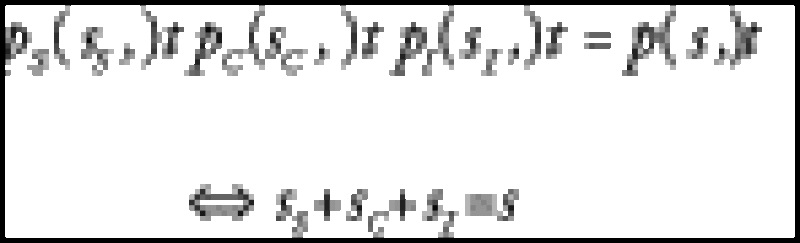
The systemic factor can generate only two states: default with probability pS, and survival with probability (1-pS). Integrating over XS yields:
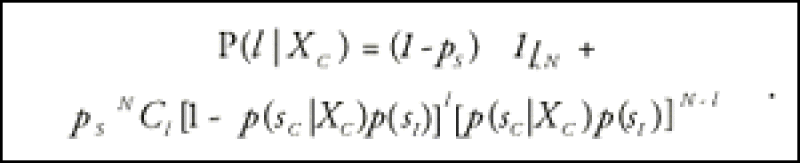
Finally, we can integrate over XC in the usual Gaussian copula fashion. Given the density g(Xc):
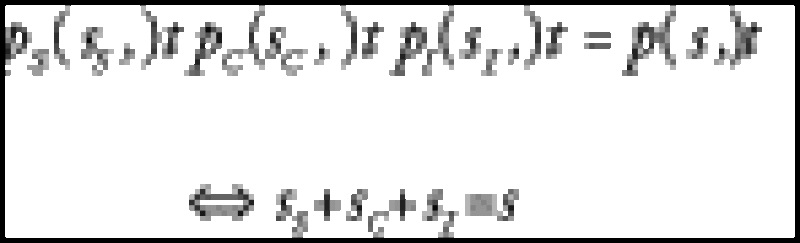
As before, in the more generic case of multiple survival probabilities and loss amounts more complex calculation methods have to be employed. However, the conditioning steps still hold true, given that the probabilities are adjusted in the correct fashion, as shown above.
Given the loss density function P(l,p1,...pN) of a basket of N independent assets with survival probabilities p1, through pN, the loss distribution conditioned on the copula factor becomes:
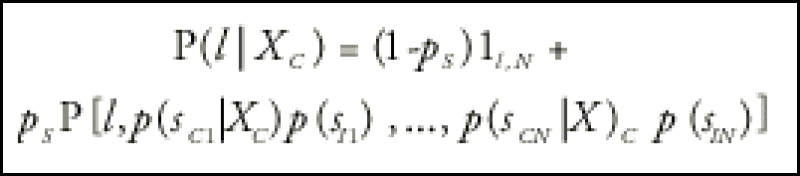
where 1l,N is the indicator function. We can generalise these expressions quite easily to multiple systemic sectors.
In Part Two
In this article we described the Composite Basket Model and showed how it can be implemented. In next week's issue we will show how the model can be calibrated to the tranche market and present some results that indicate that the model can extrapolate to different maturities and spread levels. We will also present some preliminary results that suggest that the model is useful in extrapolating to first-to-default baskets. These results strongly suggest that the model is also applicable to the pricing of bespoke baskets.
This week's Learning Curve was written by Pedro Tavares, head of quantitative analytics, Thu-Uyen Nguyen, director responsible for new product development, Alexander Chapovsky, quantitative analytics and Igor Vaysburd, quantitative analytics at Merrill Lynch.
References
1 L. Andersen and J. Sidenius, "Extensions to the Gaussian copula: random recovery and random factor loadings", Bank of America, Jun. 2004
2 S. Galiani, "Copula functions and their applications in pricing and risk managing multiname credit derivative products", King's College London, Sep. 2003
3 D. Lando, "On Cox Processes and Credit Risky Securities", www.defaultrisk.com, Mar. 1998
4 J. Laurent and J. Gregory, "Basket default swaps, CDO's and factor copulas", www.defaultrisk.com, Sep. 2003
5 L. McGinty, E. Beinstein, R Ahluwalia and M. Watts "Introducing Base Correlations", JPMorgan, Mar. 2004






